
The degree of the numerator is 1 and the degree of the denominator is 1. The \( y \) intercept is at the point \( (0, f(0)) = (0, -1) \).Ĭ - The vertical asymptote is given by the zero of the denominator \( x = 1\). The x intercept is at the point \( (-1, 0) \).
Let \( f \) be a rational function defined byī - Find the \( x \) and \( y \) intercepts of the graph of \( f \).Ĭ - Find the vertical and horizontal asymptotes for the graph of \( f \) if there are any.ĭ - Use your answers to parts a, b and c above to sketch the graph of function \( f \).Ī - The domain of \( f \) is the set of all real numbers except \( x = 1\), since this value of \( x \) makes the denominator zero.ī - The \( x \) intercept is found by solving \( f (x) = 0 \) or \( x+1 = 0\). \( m \) is the degree of the polynomial in the numerator and \( n \) is the degree of the polynomial in the numerator.Ĭase 1: For \( m \lt n \), the horizontal asymptote is the line \( y = 0 \).Ĭase 2: For \( m = n \), the horizontal asymptote is the line \( y = a_m / b_n \)Ĭase 3: For \( m \gt n \), the graph has no horizontal asymptote. Let \( f \) be a rational function defined as follows In general, the line \( y = b \) is a horizontal asymptote for the graph of \( f \) if \( f (x) \) approaches a constant \( b \) as \( x \) increases or decreases without bound. Therefore \( f(x) \) takes values close to \( \dfrac = 2 \). Horizontal Asymptotes of Rational Functionsġ) Let \( x \) increase and find values of \( f (x) \).Ģ) Let \( x \) decrease and find values of \( f (x) \).Īs \( | x | \) increases, the numerator is dominated by the term \( 2 x \) and the numerator has only one term x. In general, the line \( x = a \) is a vertical asymptote for the graph of f if \( f (x) \) either increases or decreases without bound as x approaches a from the right or from We say that the line \( x = 3 \), broken line, is the vertical asymptote for the graph of \( f \). Let us now evaluate \( f \) at values of \( x \) close to 3 such that \( x \gt 3\).ġ) As \( x \) approaches 3 from the left or by values smaller than 3, \( f (x) \) decreases without bound.Ģ) As \( x \) approaches 3 from the right or by values larger than 3, \( f (x) \) increases without bound. Let us evaluate function \( f \) at values of \( x \) close to 3 such that \( x \lt 3 \). However we can try to find out how does the graph of \( f \) behave close to The domain of \( f \) is the set of all real numbers except 3, since 3 makes the denominator equal to zero and the division by zero is not allowed in mathematics.
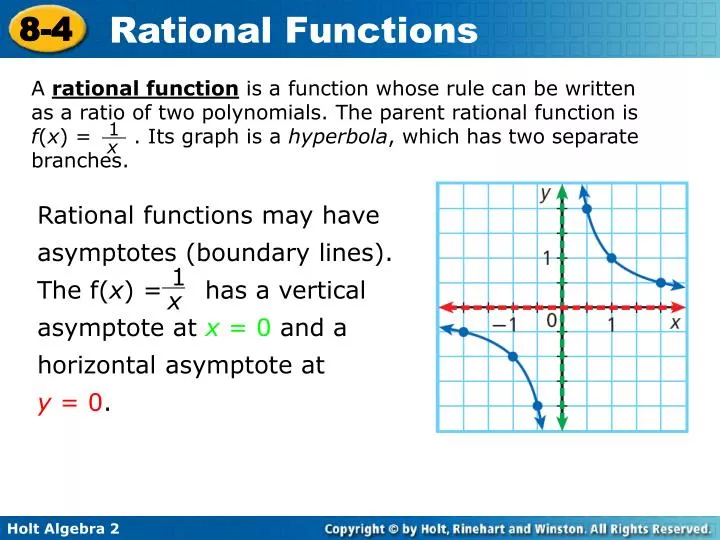
Vertical Asymptotes of Rational Functions In what follows, we assume that \( g (x) \) and \( h (x) \) have no common factors. The domain of \( f \) is the set of all real numbers except the values of \( x \) that make the denominator \( h (x) \) equal to zero. Where \( g (x) \) and \( h (x) \) are polynomial functions. The properties such as domain, vertical and horizontal asymptotes of a rational function are also investigated.
Graphing rationa fx equation how to#
How to graph a rational function? A step by step tutorial.


 0 kommentar(er)
0 kommentar(er)
